Lugar de las raíces#

Introducción#

Muchos problemas de control consisten en analizar la respuesta de un sistema cuando varía un parámetro \(k\) de la función de transferencia del sistema.

fig1.png

Figura 40 Diagrama en bloques de un sistema con un parámetro variable \(k\)#

Un ejemplo de esto son las funciones de transferencia siguientes, donde en un caso de \(G_1(s)\) el parámetro que varía es el parámetro \(k\) y en el caso de de \(G_2(s)\) el parámetro que varía es \(b\)

\[ \begin{matrix} G_1(s)= \frac{k(s+20)}{s^2+10s} & G_2(s)=\frac{1}{2s^2+bs+3} \end{matrix} \]
fig2.png

Figura 41 Diagrama en bloques de los sistema \(G_1(s)\) y \(G_2(s)\)#

Una solución práctica a este problema es evaluar el parámetro variable para distintos valores fijos y de esa forma calcular la ubicación en el plano s, de los polos y ceros, para deducir la respuesta temporal del sistema.

Y si lo anterior se pudiera hacer para todos los valores de \(\ell \in \mathbb{R}\)!. Bueno aquí, es donde entra Walter R. Evans y el «Método de Evans», que permite resolver en forma gráfica las funciones del tipo \(1+\ell~F(s)=0\) donde \(F(s)\) es una función de transferencia de la forma \(F(s)= \frac{N(s)}{D(s)}\) y \(\ell \in \mathbb{R}\), notar que de lo anterior es posible expresar lo de la forma \(D(s)+\ell~N(s)=0\). A estos gráficos o diagramas, en control, les llamamos Lugar de las raíces o en ingles Root Locus.

Este resultado lo usaremos para responder básicamente dos preguntas: ¿Cómo puedo elegir el parámetro \(\ell\) para que la respuesta dinámica del sistema cumpla con los requerimientos de performance necesarios para el sistema a controlar? y ¿Qué efecto tiene sobre la dinámica de un sistema, la variación de un parámetro \(\ell\) de su función de transferencia?

Para comenzaremos a responder estas preguntas, analizaremos el siguiente esquema «genérico» de control a lazo cerrado del sistema de la figura siguiente, donde \(k D(s)\) es el controlador del sistema con ganancia \(k\), como parámetro variable, en principio comenzaremos con \(k>0\), pero si bien, en la mayoría de los problemas que veremos \(k\) es positivo,no hay restricciones con respecto a al valor de \(k\).

fig3.png

Figura 42 Sistema genérico a lazo cerrado#

El diagrama en bloques equivalente, se reduce a:

fig4.png

Figura 43 Diagrama equivalente del sistema a lazo cerrado#

La función de transferencia a lazo cerrado es:

\[T(s)=\frac{Y(s)}{R(s)}=\frac{k D(s) G(s)}{1+k D(s) G(s)}\]

donde,

\[ G(s) = \frac{N_G(s)}{D_G(s)}=\frac{\prod_{i=1}^{m_G}(s+z_i)}{\prod_{j=1}^{n_G}(s+p_j)}\]

y

\[ D(s) = \frac{N_D(s)}{D_D(s)}=\frac{\prod_{i=1}^{m_D}(s+z_i)}{\prod_{j=1}^{n_D}(s+p_j)}\]

Los polos y ceros de \(G(s)\) son la solución de \(N_G(s)=0\) y \(D_G(s)=0\) respectivamente, y los polos y ceros de \(D(s)\) son la solución de \(N_D(s)=0\) y \(D_D(s)=0\).

La función de transferencia a lazo cerrado se puede representar de la siguiente forma:

\[T(s)=\frac{k N_D(s) N_G(s)}{D_D(s) D_G(s)+k N_D(s) N_G(s)}\]

Resultado importante

En \(T(s)\) se puede ver que los ceros a lazo cerrado no se «mueven», es decir son siempre los mismos al cambiar el valor del parámetro \(k\), pero los polos a lazo cerrado sí

\[\begin{split} \begin{matrix} \text{ceros} \quad T(s) &\Longrightarrow & k N_D(s) N_G(s) = 0 \\ \text{polos} \quad T(s) &\Longrightarrow & D_D(s) D_G(s)+k N_D(s) N_G(s)=0 \end{matrix} \end{split}\]

Ejemplo de lugar de las raíces#

Consideremos \(G(s)= \frac{1}{s+10}\) y \(D(s)= k \frac{(s+20)}{s}\) donde \(k\) es el parámetro variable, para este problema nos interesa determinar los polos y ceros del sistema a lazo cerrado y compararlos con los de la funciones a lazo abierto, por lo que consideraremos que \(k=2\)

\(D(s)\) tiene un polo y un cero en: \(p_1=0\) y \(z_1=-20\)

\(G(s)\) tiene solo un polo en: \(p_2=-10\)

k=2
D=ctrl.tf([1, 20],[1,0])
G=ctrl.tf([1],[1,10])
T=ctrl.feedback(k*D*G)
ceros_lc=T.zero()
ceros_lc

array([-20.+0.j])

polos_lc=T.pole()
polos_lc

array([-6.+2.j, -6.-2.j])

\(T(s)\) tiene un cero en: \(z_1=-20\)

\(T(s)\) tiene un par de polos complejos conjugados en: \(p_{1,2}=-6\pm 2j\)

Repaso de espacio vectorial complejo: Vector complejo#

Veremos la representación vectorial de números complejos, para lo que partiremos de número complejo \(\overrightarrow{s}= \sigma + j \omega\), cuya representación vectorial es la siguiente:

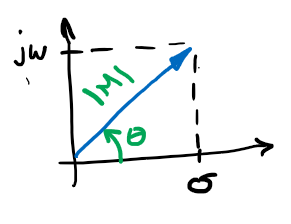
fig5.png

Figura 44 Vector \(\overrightarrow{s}= \sigma + j \omega\)#

donde,

\[|M|=\sqrt{\sigma^2+\omega^2}\]
\[ \theta= \arctan{\frac{\omega}{\sigma} }\]

ahora consideremos que tenemos el vector \(\overrightarrow{v} = \overrightarrow{s} + a\) con \(a \in \mathbb{R}\) y \(\overrightarrow{s} = \sigma + j \omega \in \mathbb{C}\), la traslación de \(\overrightarrow{s}\), cuya representación es:

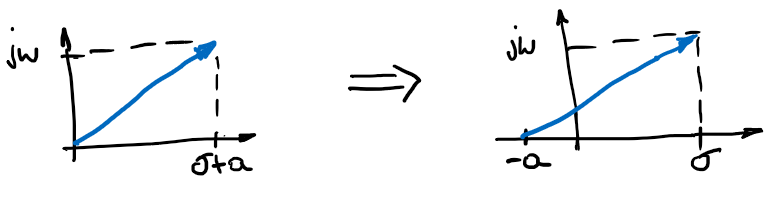
fig6.png

Figura 45 Vector \(\overrightarrow{v}\)#

en general, podemos decir que si que si tenemos la función de transferencia \(F(s)\) donde \(s\) es la variable compleja y con polos y ceros, tal que:

\[F(s) = \frac{\prod_{i=1}^{m}(s+z_i)}{\prod_{j=1}^{n}(s+p_j)}\]

podemos halla el módulo de \(F(s)\) haciendo,

\[|F(s)|=\frac{\prod \text{mod. ceros}}{\prod \text{mod. polos}}= \frac{\prod_{i=1}^{m}|s+z_i|}{\prod_{j=1}^{n}|s+p_j|}\]

y el argumento de \(F(s)\) será,

\[ \angle{F(s)}= \sum{ang. ceros}-\sum{ang. polos}= \sum_{i=1}^{m}{\angle{(s+z_i)}}-\sum_{j=1}^{n}{\angle{(s+p_j)}}\]

Ejemplo punto de prueba#

Supongamos un punto de prueba fijo en el plano-s \(s_0=-1+j\) y la función de transferencia,

\[F(s)=\frac{1}{s(s+d)}\]

Calcularemos el módulo y el argumento de \(F(s_0)\)

\[|F(s_0)|= \frac{1}{\sqrt{s}\sqrt{s}}=\frac{1}{2}\]
\[\angle{F(s_0)}=\underbrace{0}_{\sum{\angle(s+z_i)}}-\underbrace{(45º+135º)}_{\sum{\angle{(s+p_j)}}}=-180º\]
\[F(s_0)= \frac{1}{2} \angle{-180º}\]
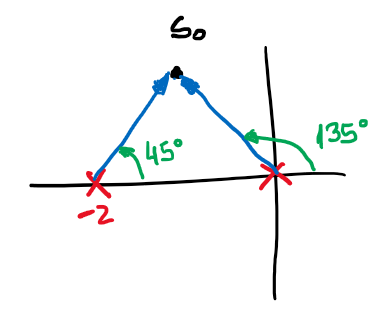
fig7.png

Figura 46 Módulo y argumento de \(F(s_0)\)#

Ejemplo: Trazado del lugar de las raíces#

En el siguiente ejemplo mostraremos la ubicación de los polos de \(G(s)\) para distintos valores de la variable \(k\), consideraremos \(k>0\), cuando se cierra el lazo con realimentación unitaria, como se muestra en la siguiente figura:

fig8.png

Figura 47 \(G(s)\) a lazo cerrado con un controlador proporcional \(D(s)=k\)#

entonces calculamos la función de transferencia a lazo cerrado \(T(s)\):

\[T(s)=\frac{k}{s^2+10s+k}\]

los polos de \(T(s)\) son la raíces de la ecuación característica del sistema

\[ \begin{matrix} \underbrace{s^2+10s+k}_{2^{do}\text{ orden}~ \Rightarrow ~ \text{2 polos}}=0 & \text{con} & k: 0\longrightarrow \infty \end{matrix} \]

para esto haremos una tabla y calcularemos las raíces de la ecuación característica para distintos valores de \(k\) de la forma \(s_{1,2}=\frac{-b \pm \sqrt{b^2-4ac}}{2a}\):

k

polo 1

polo 2

\(0\)

\(-10\)

\(0\)

\(\vdots\)

\(\vdots\)

\(\vdots\)

\(25\)

\(-5\)

\(-5\)

\(\vdots\)

\(\vdots\)

\(\vdots\)

\(>25\)

\(-5 + j x\)

\( -5-jx\)
fig9.png

Figura 48 Lugar de las raíces de \(G(s)\)#

Propiedades de el Lugar de las Raíces#

El lugar geométrico de las raíces, es el lugar geométrico de valores de \(s\) para el cual la ecuación característica \(1 + kD(s)G(s) = 0\), ya que el parámetro \(k \in \mathbb{R}\) varía desde \(0 \longrightarrow \infty\).

\[T(s)=\frac{k D(s) G(s)}{1+k D(s) G(s)}\]

Los polos de \(T(s)\) existen cuando el polinomio característico \(1 + k D(s)G(s)\) se anula, es decir,

\[ k D(s) G(s) = -1 = 1 \angle{2 \ell +1}\pi\]

con \(\ell = 0 \pm 1, \pm 2, \pm 3, \dots\)

o lo que es lo mismo:

\[\begin{split} \left\{\begin{array}{l} |k D(s) G(s)|=1\\ \angle{k D(s) G(s)} = \angle{2 \ell +1}\pi \end{array}\right. \end{split}\]

Teniendo en cuanta que la función compleja la podemos discriminar en su magnitud y fase, y para \(k>=0\), podemos arribar a la siguientes definiciones:

Condición de fase

El lugar geométrico de las raíces de \(D(s)G(s)\) es el lugar geométrico de puntos en el plano-\(s\) donde la fase de \(D(s)G(s)\) es 180.

Esto se lo conoce como la condición de fase, que significa matemáticamente:

\[\angle G(s) = 180^o+\ell.360^o,\quad \text{con } \ell \text{ entero.}\]

Condición de magnitud o de módulo#

El criterio de magnitud es el siguiente que lo obtenemos aplicando el módulo a la ecuación \(1+KG(s)=0\). Entonces resulta:

\[\|D(s) G(s)\|=\frac{1}{|k|}\]

y para \(k>0\):

\[k=\frac{1}{\|D(s)\| \|G(s)\|}\]

Este criterio nos permite determnar el \(k\), una vez escogido una ubicación determinada del lugar geométrico de las raíces.

Ejemplo de cálculo de k con la condición de módulo#

si \(p_1 = p_2 = -5\) un punto del plano s que cumple con la condición de fase para la función de transferencia \(G(s)=\frac{1}{s(s+10)}\)

Calculamos el modulo \(|G(p_1)|= \|\frac{1}{-5(-5+10)} \| =\frac{1}{25}\) por lo que por la condición de módulo es:

\[k=\frac{1}{|G(p_1)|}= 25\]

Este valor es el que corresponde al ejemplo anterior (ver tabla de valores y raíces)

Ejemplo: cálculo de fase para un punto especifico del plano-s, \(s_0\)#

Tenemos la siguiente función de transferencia G(s) a lazo abierto:

\[G(s)=\frac{s+1}{s\left\{\left[\left(s+2\right)^2+4\right]\left(s+4\right)\right\}}\]
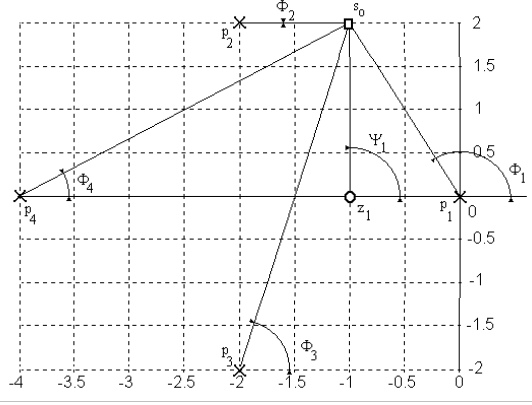
fig10.png

Figura 49 \(G(s)\) en un punto del plano-s genérico \(s_0\)#

En la figura anterior mostramos con cruces la ubicación de los polos de esta función de transferencia, y con círculos los ceros. Suponemos un punto de prueba ubicado en \( s_o = -1 + 2j \), y realizamos la suma de las contribuciones de las fases para determinar si es o no punto del lugar de raíces:

\[\begin{split} \begin{matrix} \angle G(s) &= & \Psi_1 - \Phi_1- \Phi_2- \Phi_3- \Phi_4\\ & = & 90^o -116.6^o -0^o -76^o - 33.7^o\\ & = & -136.3^o \end{matrix} \end{split}\]

La fase de \( G \) para este punto de prueba vale \( -136.3^o \), y no \( 180^o \) por lo tanto este punto de prueba no pertenece al lugar geométrico de las raíces.

Nota

Para verificar este punto con Python debemos evaluar la función transferencia en el punto de interés y el ángulo de valor resultante.

  s=ctrl.tf('s')
  G=(s+1)/(s*((s+2)**2+4)*(s+4))
  ang=np.angle(G(-1+2j))*180/np.pi
  print(ang)

Mostramos este código en acción y vemos el resultado:

s=ctrl.tf('s')
G=(s+1)/(s*((s+2)**2+4)*(s+4))
ang=np.angle(G(-1+2j))*180/np.pi
print(ang)

-136.21887523513132

Ejemplo cálculo de la condición de magnitud#

Supongamos tener la transferencia siguiente:

\[G(s)=\frac{1}{s(s^2+4s+8)}\]

cuyas polos se ubican en el origen y en \(-2\pm 2j\). En la figura siguiente mostramos el lugar de las raíces para esta función de transferencia.

Elegimos un punto de prueba en \(-0.667 \pm 2j\), que pertenece al lugar geométrico de las raíces, pues ese punto cumple con ciertos requerimientos para nuestro sistema de control.

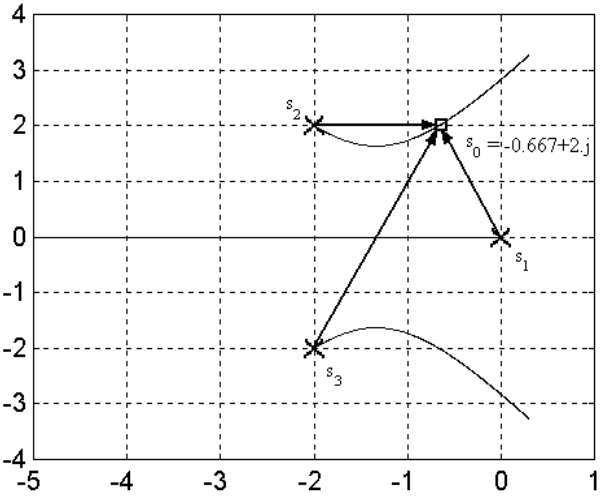
fig11.png

Figura 50 \(G(s)\) en un punto del plano-\(s\) genérico \(s_0\)#

Entonces determinamos la ganancia \(K\) para llegar a ese punto como:

\[k=\frac{1}{|G(s)|}=|s_0||s_0-s_2||s_0-s_3|\]
\[k=2.108\cdot1.33\cdot4.216=11.85\]

Verificamos el cálculo usando Python

G=1/((s+2-2j)*(s+2+2j)*s)
k=1/np.abs(G(-0.6667+2j))
print(k)

11.851585185962918